Methods in transport geography

Today

  • 15 minute window into statistical methods

  • Transport geography

  1. Spatial network from the graph theory perspective

  2. Spatial Interaction and Gravity Model

  3. Accessibility

15 minute window into statistical methods

  • Regression/Linear Regression

15 minute window into statistical methods

Regression/Linear Regression - describes the strength and character of an association between two or more variables

15 minute window into statistical methods

Regression/Linear Regression

\(Y_i = \beta_0 + \beta_1 X_i + \varepsilon_i\)

Regression assumptions

  1. Linearity - The relationship between X and the mean of Y is linear.

  2. Homoscedasticity - The variance of residual is the same for any value of X.

  3. Independence - Observations are independent of each other

Demonstration

Transport geography: quantitative dimension

  • Why transport in this module?

  1. Fundamental for social and economic activities

  2. All about networks & interactions

Transport geography: key elements

  • Distance

  • Accessibility: the capacity of a location to be reached by, or to reach different locations

  • Spatial interaction: movement of people, freight or information between an origin and destination

  • Transportation and land use models

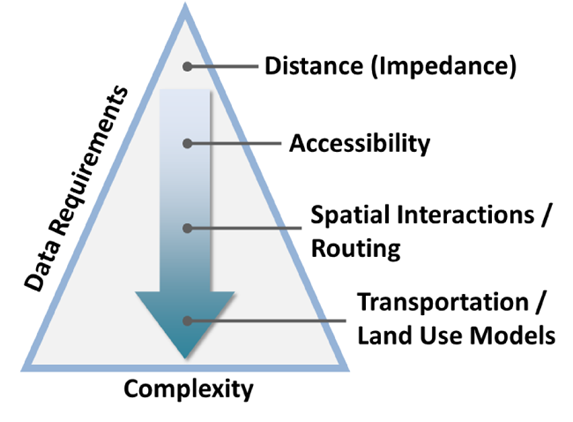
Source: Rodrigue (2020)

Spatial network from the graph theory perspective

Source: Wu et al. (2019)

Spatial network from the graph theory perspective

Terminology

  • terminal = node = vertex

  • link = edge

  • Sub-graph - Loop (buckle)

More types of graphs

  • Planar graph vs Non-planar graph

  • Cycle, circuit

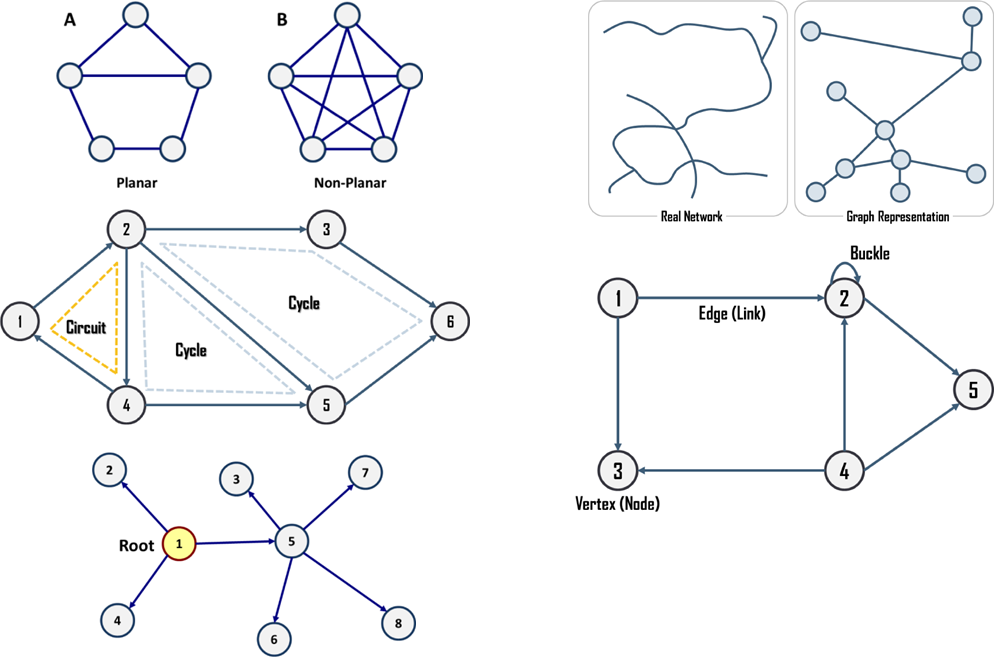Source: Rodrigue (2020)

Plannar graph analysis

  • Proportion between nodes and edges: \(\beta = e / v\), where \(e\) is the number of links & \(v\) the number of nodes

  • Network density: \(Gamma\) AKA (number of liks / maximum number of links)

    • planar: \(\gamma = \frac{e}{3(v-2)}\)

    • non-planar: \(\gamma = \frac{2e}{v(v-1)}\)

  • Structure vs Topology

Plannar graph analysis

  • Degree centrality, Betweenness, Eigenvector centrality,…

  • Eccentricity: the distance from a given node to the farthest node from it in the network

  • Shimbel index, or nodal accessibility, or Fareness (see Lecture 3

    • \(c_đť‘–= \sum_j d_{ij}\)

    • This is a purely topological accessibility metric, remember this for later.

Graph analysis

Closeness centrality (from Lecture 3)

  • Which node has the shortest distance to other nodes

  • Instead of focusing on the number of links, the focus turns to the network distances

  • Different definitions:

  • Closeness, \(c_{i} = 1/\sum_{j} d_{ij}\)

  • Fareness, \(c_{i} = \sum_{j} d_{ij}\)

  • igraph calculates closeness

Graph analysis

The Gini coefficient

  • Measure of dispersion often used as Inequality measure

    • 0: perfect equality
    • 1 :perfect inequality

  • Ordered X and Y, cumulative percentage

  • Mostly used for income inequalities, but can be more widely used

  • \(Gini = A / (A + B)\)

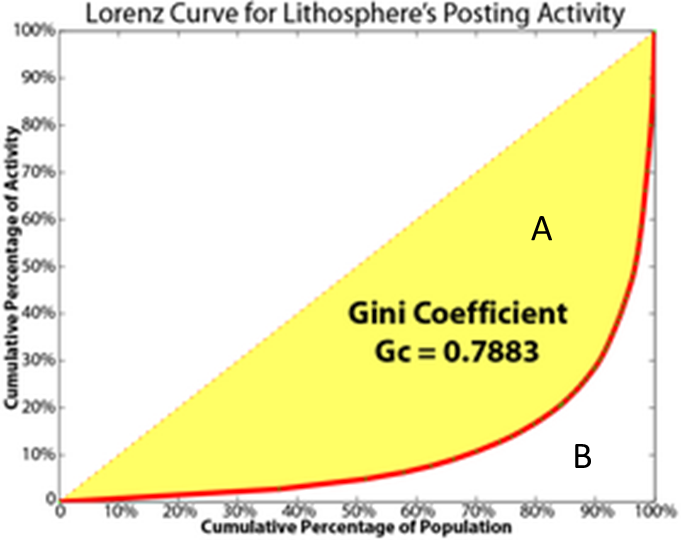
Source: Rodrigue (2020)

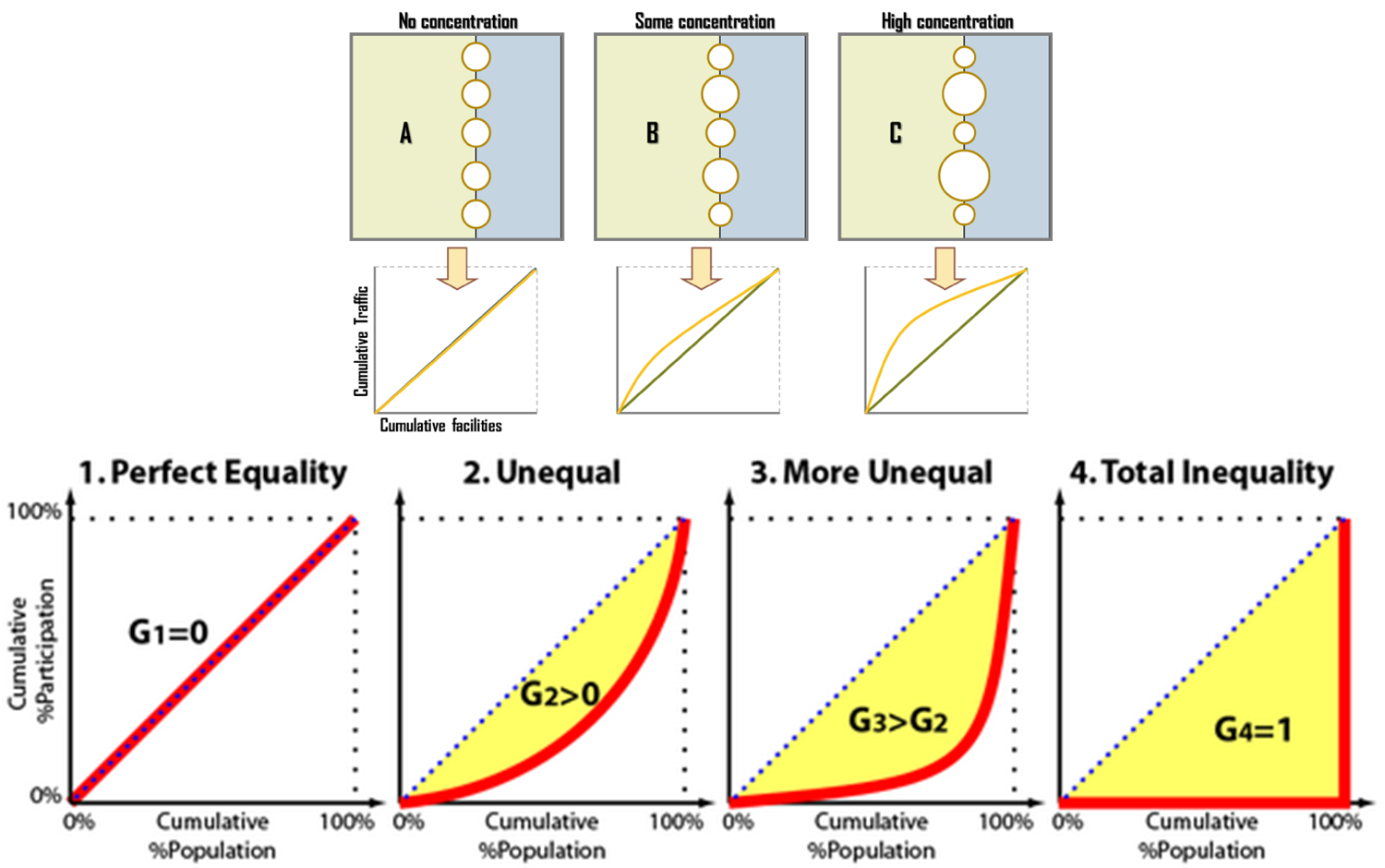Source: Rodrigue (2020)

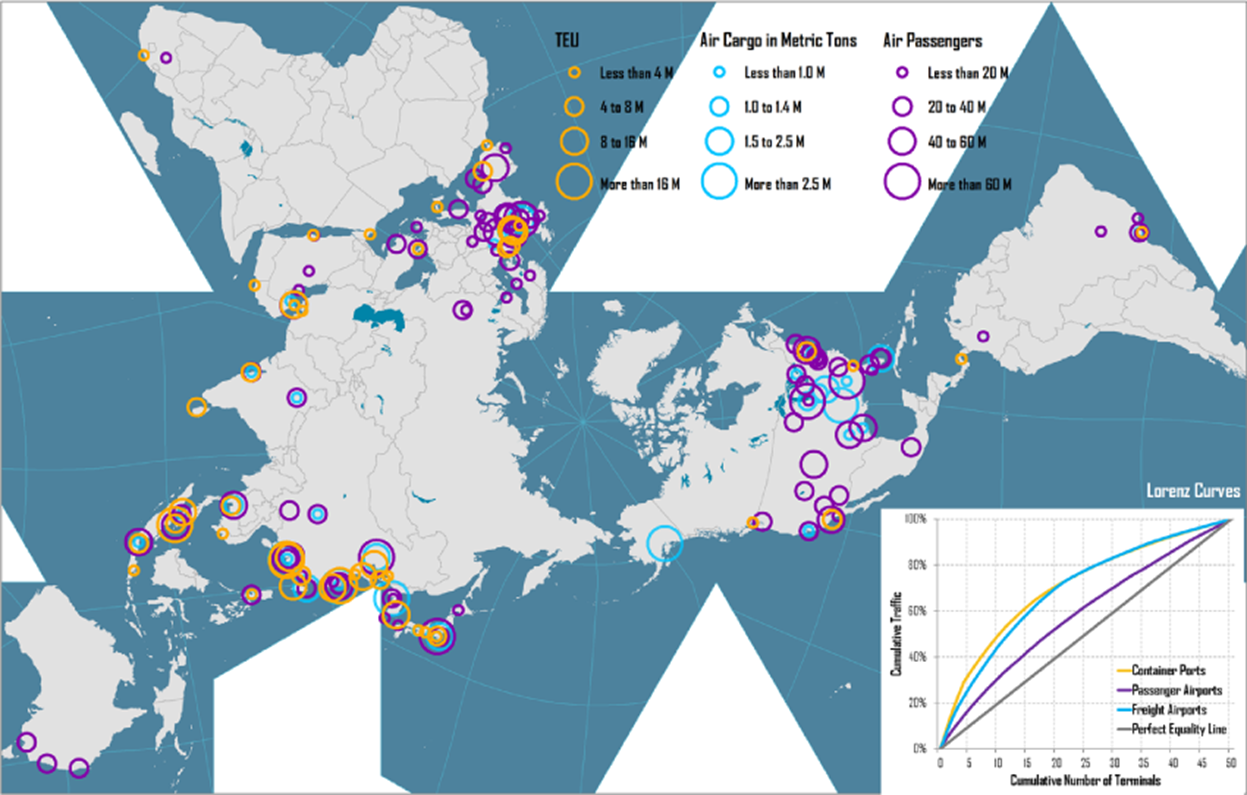Source: Rodrigue (2020)

Example: measuring traffic concentration

Temporal variations of the Gini coefficient reflect changes in the comparative advantages of a location within the transport system

Spatial interactions and the gravity model

  • A spatial interaction is a realised movement of people, goods or information between an origin and a destination

  • It is a transport demand/supply relationship expressed over geographical space.

Spatial interactions and the gravity model

Conditions for spatial interaction to be materialised

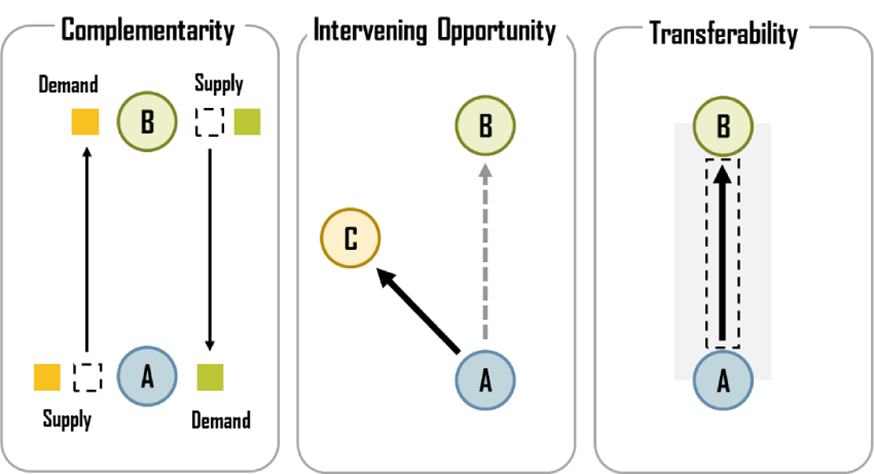Source: Rodrigue (2020)

Spatial interactions and the gravity model

Spatial interactions and the gravity model

Gravity model

Analogy of Gravity model

\(Force_{ij} = G \frac{Mass_i Mass_j}{Dist_ij}\)

\(Flow_{ij} = \frac{Attribute_i Attribute_j}{Separation_{ij}}\)

Spatial interactions and the gravity model

\(T_{ij} = f(V_i, W_j, S_{ij})\)

  • Flows are a function of the attributes of the locations of origin, the attributes of the locations of destination and the friction of distance between the concerned origins and the destinations

  • \(T_{ij}\): Interaction between location \(i\) (origin) and location \(j\) (destination)

  • \(V_i\): Attributes of the location of origin \(i\) (e.g. population, number of jobs available, industrial output, GDP); push factors; the potential of origins

Spatial interactions and the gravity model

\(T_{ij} = f(V_i, W_j, S_{ij})\)

  • \(W_j\): Attributes of the location of destination \(j\), pull factors; attractiveness of destinations

  • \(S_{ij}\): Attributes of separation between \(i\) and \(j\) (e.g. distance, transport costs, or travel time); cost of overcoming the separation between origins and destinations

Spatial interactions and the gravity model

\(T_{ij} = k\frac{V_i^\lambda W_j^\alpha}{d_{ij}^\beta}\)

  • \(\beta\): transport friction parameter

  • \(\lambda\): Potential to generate movements

  • \(\alpha\): Potential to attract movements

What can we do with this?

1. Calculate flows (naive)

\(T_{ij} = k\frac{V_i^\lambda W_j^\alpha}{d_{ij}^\beta}\)

  • Known: \(V\), \(W\), and \(d\)

  • Define: \(\lambda=1\), \(\alpha=1\), \(\beta=2\), and \(k=0.00001\)

  • These are some standard results from past empirical studies

  • Big unknown: \(T\)

  • Example from Tranos, Gheasi, and Nijkamp (2015)

1. Calculate flows (naive)

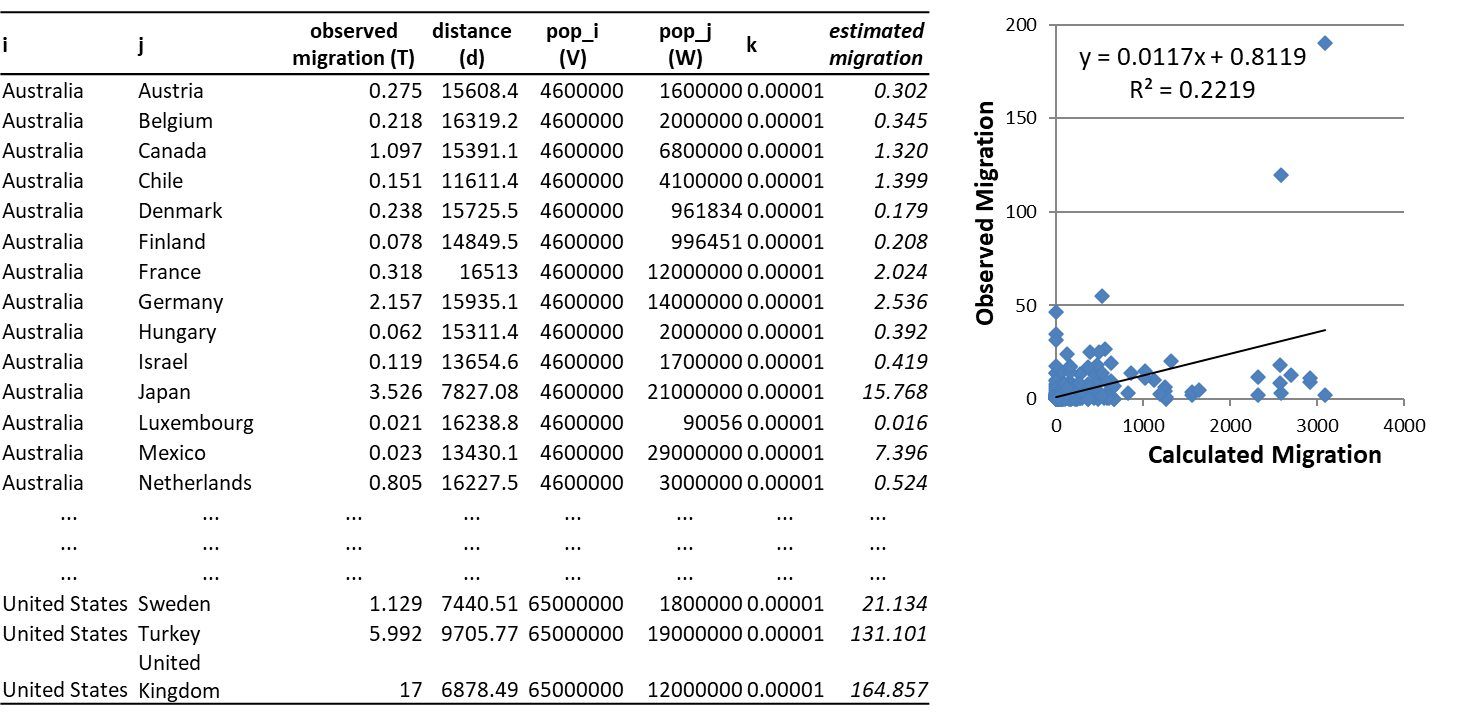
1. Calculate flows (naive)

  • Fairly good estimation of reality for such an oversimplified model, but…

  • … not good enough.

2. Estimate \(\lambda\), \(\alpha\), \(\beta\) and \(k\)

  • Known: \(T\), \(V\), \(W\), \(d\) and \(k\)

  • Estiamte: \(\lambda=1\), \(\alpha=1\), and \(\beta=2\)

  • Why? To understand the effect of distance, pull and push factors

  • How? Regression

2. Estimate \(\lambda\), \(\alpha\), \(\beta\) and \(k\)

  • \(T_{ij} = k\frac{V_i^\lambda W_j^\alpha}{d_{ij}^\beta}\)

  • Look up properties of logarithms, e.g. here

  • \(T_{ij} = kV_i^\lambda W_j^\alpha d_{ij}^{-\beta}\)

  • \(ln T_{ij} = ln (kV_i^\lambda W_j^\alpha d_{ij}^{-\beta})\)

  • \(ln T_{ij} = lnk + lnV_i^\lambda + ln W_j^\alpha + lnd_{ij}^{-\beta}\)

  • \(\color{red}{ln T_{ij}} = \color{blue}{lnk} + \lambda \color{green}{lnV_i} + \alpha \color{orange}{ln W_j} -\beta \color{purple}{lnd_{ij}}\)

  • \(\color{red}{y} = \color{blue}{c} + \lambda \color{green}{x_1} + \alpha \color{orange}{x_2} + \beta \color{purple}{x_3}\)

  • Multivariate linear regression

2. Estimate \(\lambda\), \(\alpha\), \(\beta\) and \(k\)

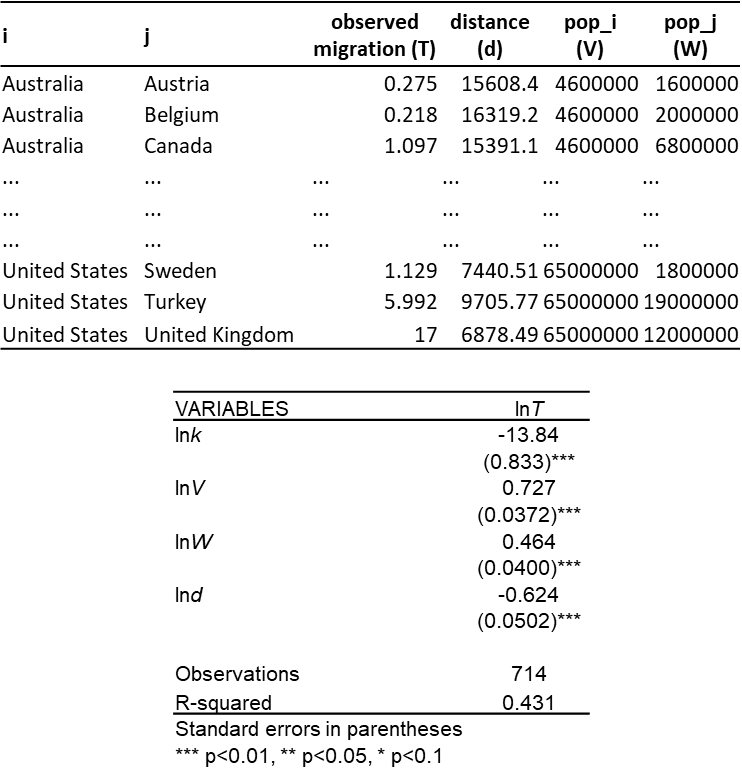
2. Estimate \(\lambda\), \(\alpha\), \(\beta\) and \(k\)

  • \(c = lnk = 13.84\)

  • \(\lambda = lnV_i = 0.727\)

  • \(\alpha = lnW_j = 0.464\)

  • \(\beta = lnd_{ij} = -0.624\)

  • What did we learn?

  • How can we use these coefficients

3. Estimate accessibility indicators

  • The potential of opportunities for interaction

  • Ease of spatial interaction

  • Attractiveness of a node in a network taking into account the mass of other nodes and the costs to reach those nodes via the network

3. Estimate accessibility indicators

Different typologies (Holl 2007)

  1. Network access

    • distance to access the network

    • travel opportunities

  2. Travel cost measures

    • network access + distance/time travelled on the network

  3. Market potential accessibility

    • destinations at greater distance provide diminishing opportunities
Source: Bruinsma and Rietveld (1998)

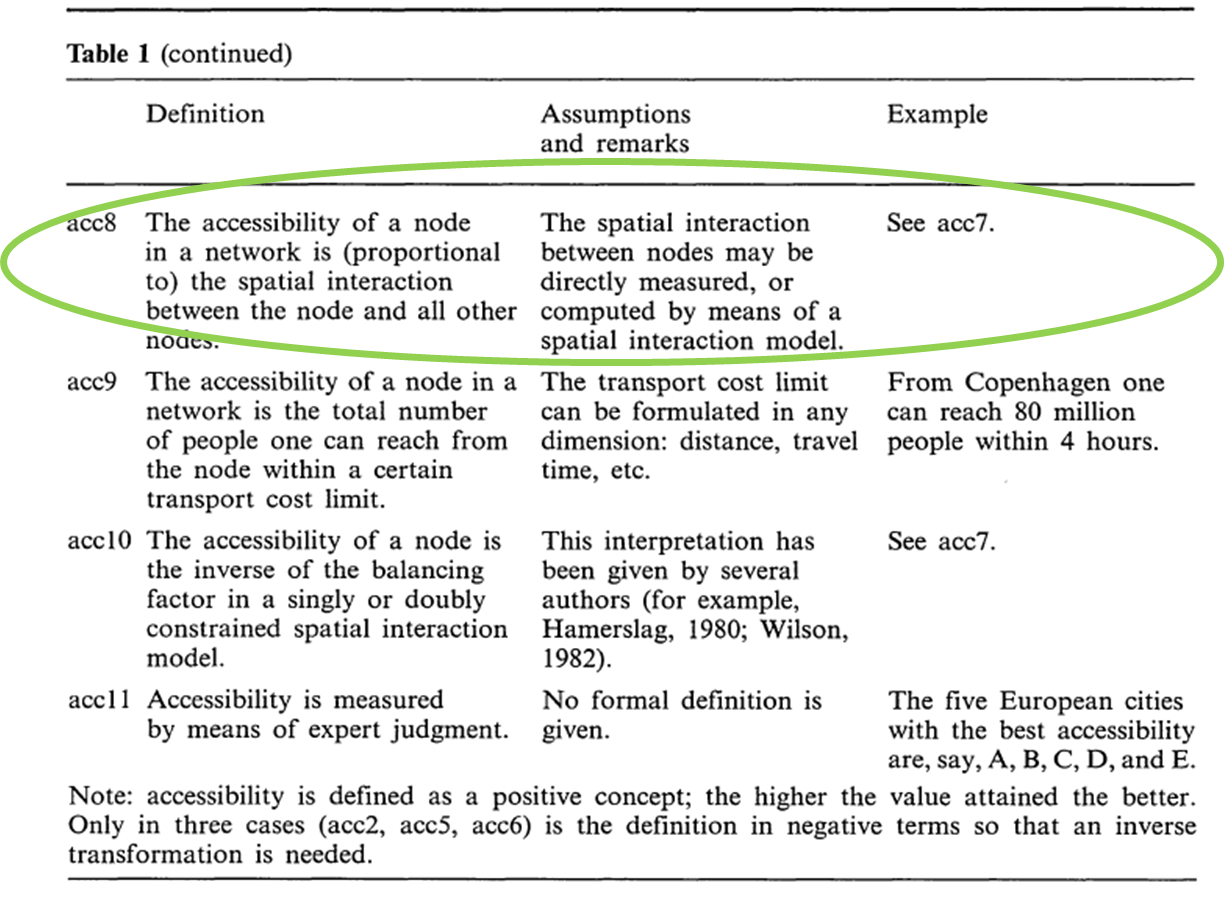
3. Estimate accessibility indicators

  • \(Acc_{i} = \sum_j \frac{W_j}{d_{ij}^2}\)

Source:Rodrigue (2020)

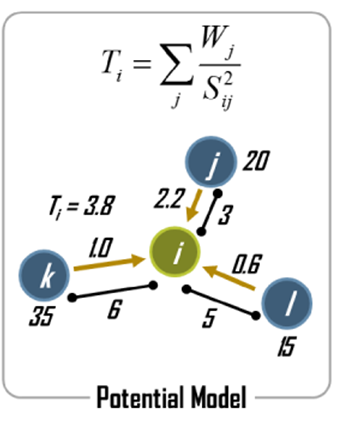
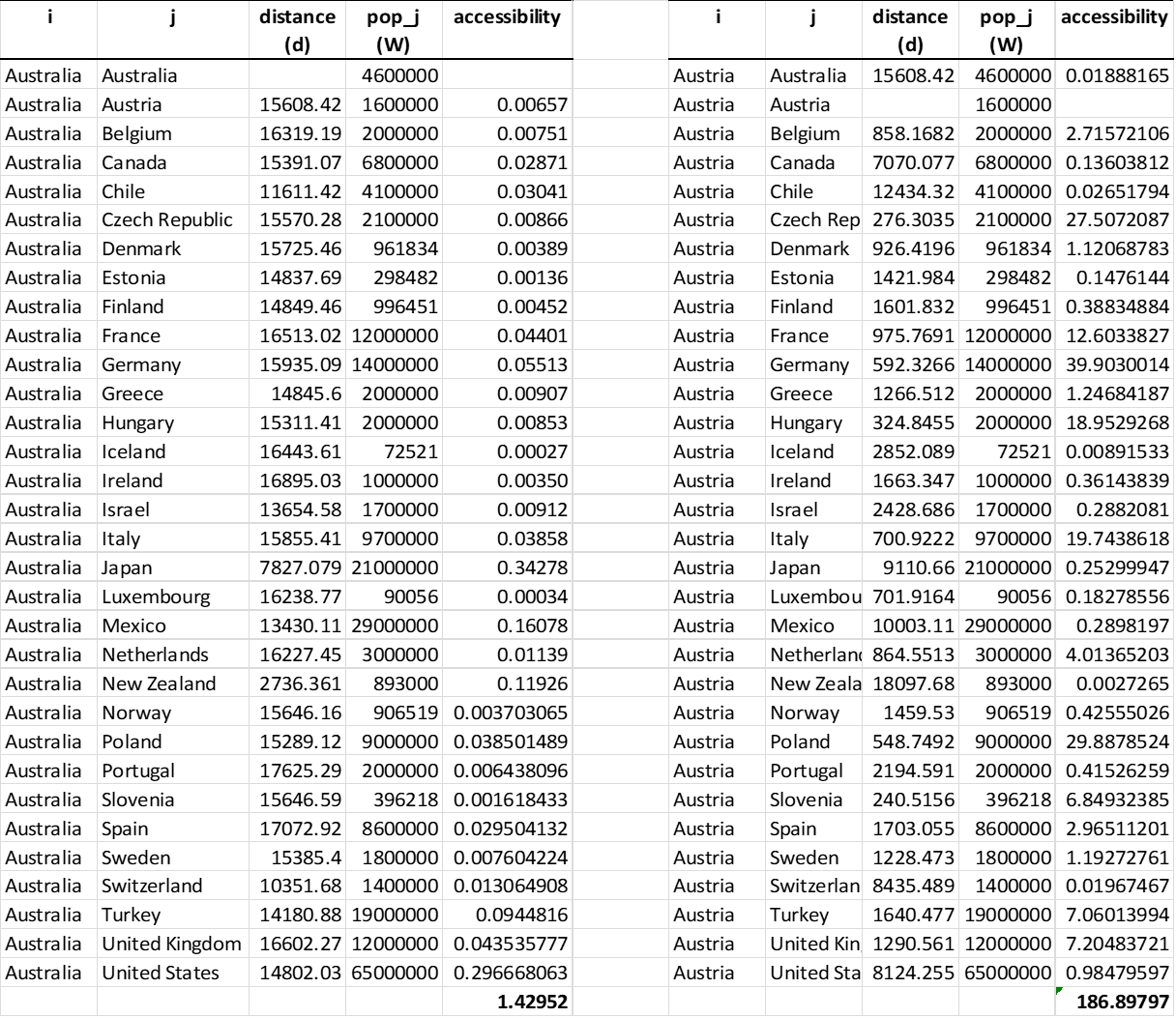
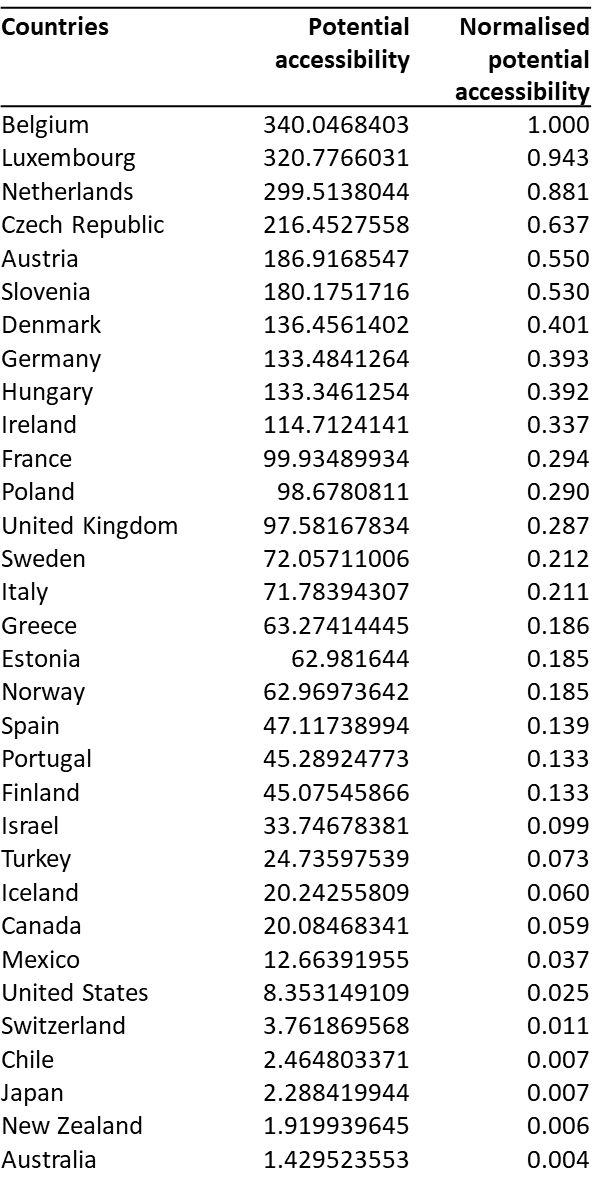
3. Estimate accessibility indicators

  • Geographical indicator

  • Spatial structure (e.g. distance) and economic activities (e.g. population)

  • The potential for interaction

  • Opportunities

Not the only way to define accessibility on networks!

Discussion: What is accessibility to you?

Accessibility of locations from routing perspective

Accessibility of locations from routing perspective

Vrabková, Ertingerová, and Kukuliač (2021)

Vrabková, Ertingerová, and Kukuliač (2021)

References

Bruinsma, Frank, and Pieter Rietveld. 1998. “The Accessibility of European Cities: Theoretical Framework and Comparison of Approaches.” Environment and Planning A 30 (3): 499–521.
Holl, Adelheid. 2007. “Twenty Years of Accessibility Improvements. The Case of the Spanish Motorway Building Programme.” Journal of Transport Geography 15 (4): 286–97. https://doi.org/https://doi.org/10.1016/j.jtrangeo.2006.09.003.
Rodrigue, Jean-Paul. 2020. The Geography of Transport Systems. Routledge. https://transportgeography.org/.
Tranos, Emmanouil, Masood Gheasi, and Peter Nijkamp. 2015. “International Migration: A Global Complex Network.” Environment and Planning B: Planning and Design 42 (1): 4–22.
Vrabková, Iveta, Izabela Ertingerová, and Pavel Kukuliač. 2021. “Determination of Gaps in the Spatial Accessibility of Nursing Services for Persons over the Age of 65 with Lowered Self-Sufficiency: Evidence from the Czech Republic.” Edited by Dragan Pamucar. PLOS ONE 16 (1): e0244991. https://doi.org/10.1371/journal.pone.0244991.
Wu, Mincheng, Shibo He, Yongtao Zhang, Jiming Chen, Youxian Sun, Yang-Yu Liu, Junshan Zhang, and H. Vincent Poor. 2019. “A General Framework of Studying Eigenvector Multicentrality in Multilayer Networks.” Proceedings of the National Academy of Sciences 116 (31): 15407–13. https://doi.org/10.1073/pnas.1801378116.