Network science, urban laws and scaling

Network science, urban laws and scaling

1. Development of network science: 1980-2000 1st Milestone - regular vs random networks 2nd Milestone - small worlds 3rd Milestone - scale free networks
2. Epistemological discussion
3. What do we mean by scaling
4. The five laws of urban scaling

Network Science: The Evolution of a ‘New’ Science

• Not really new

• Graph Theory in the 18th century

• Leonhard Euler’s work on small graphs

• High degree of regularity: similar degree centrality among different nodes

Regular graphs

1st milestone: Random networks (RN)

• 20th Century: advances in mathematics and statistics

• Algorithmic network analysis

• Erdős, Rényi, et al. (1960)

• Large scale networks with no obvious structure

• Nodes degree follows a Poisson distribution: similar degree, close to the average degree , rare exceptions

• Representative of real world network?

1st milestone: Random networks (RN)

Source: Watts and Strogatz (1998)

1st milestone: Random networks (RN)

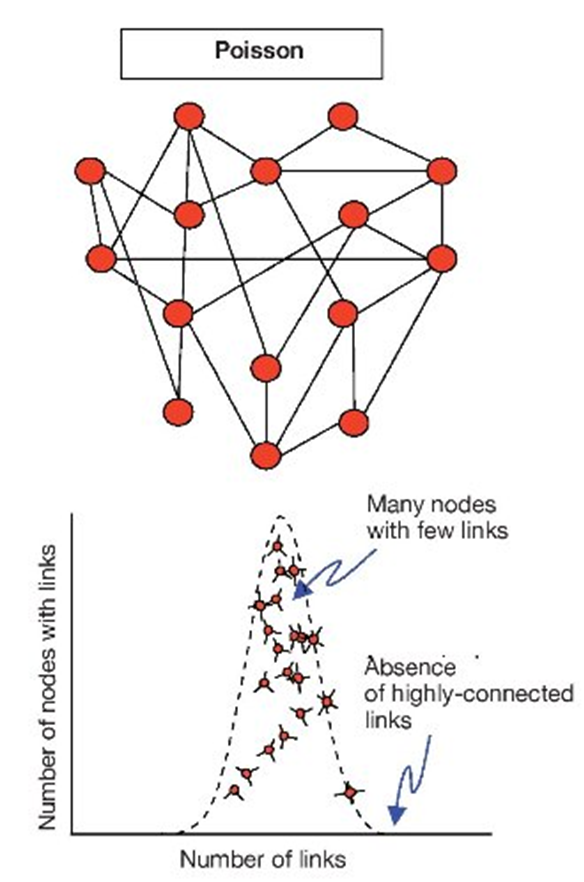
Source: Torres et al. (2009)

Networks become important…

• … in different fields, from social science to biology

• Digitization of data in many different fields + large databases ➔ real world systems as networks

• Advances in computer science and in computing

• Looseness between different disciplinary boundaries

• Reductionist approaches lose ground in favor of holistic research approaches, which try to understand the system as a whole

2nd milestone: Small-worlds

• Small world effect

• Milgram’s six degrees of separation (1967)

• Bacon number

• Short average distances, enabling nodes to reach each other within a few steps

• Characteristic of numerous real world networks

• Structural characteristic rather than an organizing principle

• Even RN networks are characterized by short average distances

2nd milestone: Small-worlds

• Watts and Strogatz (1998) Small-world (SW) model

• Coexistence of short average distance with high clustering coefficient

• SW networks are located between regular and random networks:

  • Highly clustered like regular lattices

  • Small distances like random networks

  • Node degree distribution is quite similar with the RN and decays exponentially

2nd milestone: Small-worlds

• A set of intensively interconnected local clusters, which gain global connectivity via a few links, which span the entire network linking distant clusters

• Nodes in SW networks benefit from the high local connectivity and easy distant communication with remote clusters using the intra-cluster links

• Probability of finding a highly connected node decreases exponentially as highly connected nodes are practically absent in RN and SW models

2nd milestone: Small-worlds

Source: Watts and Strogatz (1998)

2nd milestone: Small-worlds

Pros and cons

• Social capital (bridging and bonding)

• Disease spread

• Real world examples?

3rd milestone: Scale-free (SF) networks

• Barabási and Albert (1999)

• Very few super connected nodes and a vast majority of less connected nodes

• SF: nodes degree distribution follows a power law distribution regardless the scale of observation

• 2 main formation mechanisms:

  • growth: expansion of networks over time

  • preferential attachment: growth is not equally dispersed across the nodes; highly connected nodes are more likely to receive new links than the lower degree nodes

3rd milestone: Scale-free (SF) networks

• An initial difference in the connectivity between two nodes will increase further as the network grows

• This is a cumulative — rich get richer — process

• The probability \(P(k)\) that a node has a degree \(k\) decays following a power function, with usually \(2 < \gamma < 3\)

  \(P(k)≈𝑘^{−\gamma}\)

• Power laws in networks are related with the existence of both of the above two mechanisms

• Later versions of SF models included more realistic options for the network growth

3rd milestone: Scale-free (SF) networks

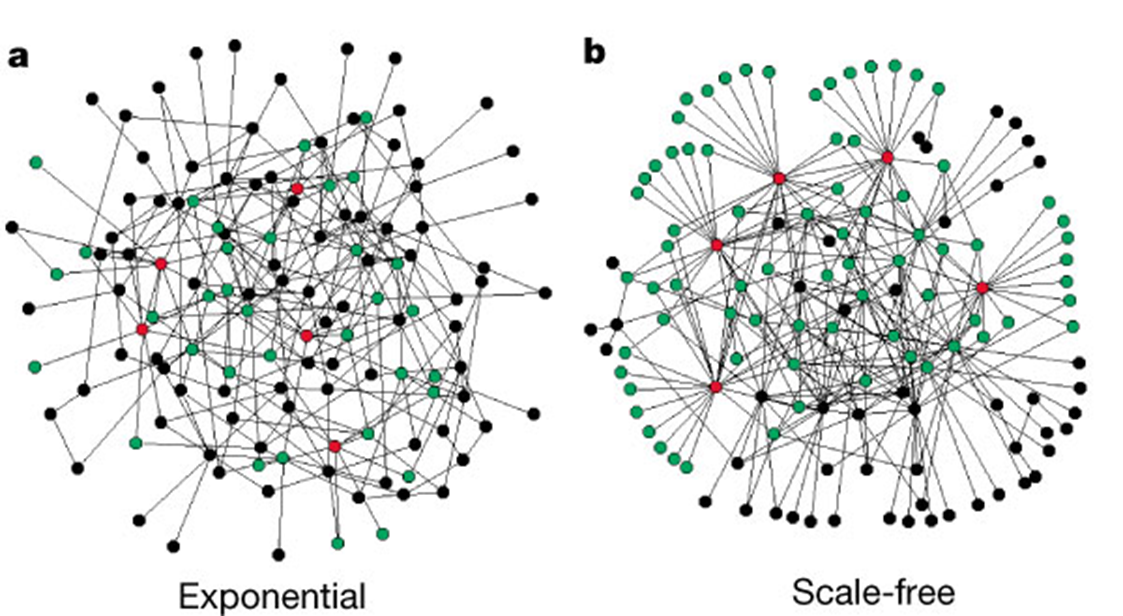
Source: Albert, Jeong, and Barabási (2000)

3rd milestone: Scale-free (SF) networks

And finally the power law…

3rd milestone: Scale-free (SF) networks

Pros and cons?

• Efficiency

• Resilience

• Disease spread prevention

• Vulnerability towards targeted attacks

• Real world examples?

Network Science: a summary

• Both RN and SW have short average distances

• RN cannot be included in SW because they lack the high clustering coefficient

• SF networks share the short average distance and the high cluster coefficient of SW ones, but the SW are not characterized by the scale-free distribution

• All scale free networks display small world properties, while all small-world networks are not necessarily scale free

Network science: An epistemological discussion

1. Complexity Science

• Most studies in the network science domain have a starting point in statistical physics

• Stochastic approaches

• Underlying probability model which usually follows a power law

• Main objective: identification of the underlying mechanisms using generative modeling and simulation

• Potential risk: the probability model might not follow a power law mechanism, which is a common assumption

Network science: An epistemological discussion

2. Social Network Analysis

• Sociology and graph theory

• Focus on social networks

• Extensive utilization of network metrics

Network science: An epistemological discussion

3. Geography and Urban Analytics

• Softer’ approaches

• Ex-post empirical modeling for identifying characteristics of theoretical network models in real world networks

• Global and local network statistics

• Use of network measures in mainstream statistical modeling

• Empirical verification of the functions that better explain the node degree distribution (power vs. exponential functions)

• Spatial networks, but also dynamic networks

Scaling

What do we mean by scaling

What do we mean by scaling

What is scale and scaling

• Scale in geography

• Scale in math:

  • \(y(x_i)\) a function of \(x_i\) where \(i\) is a spatial unit

  • If we scale \(x\) by some scalar \(\lambda\), the function scales if its scaled value is proportional to its previous value: \(y(\lambda x_i) \propto y(x_i)\)

  • \(y(x_i) = x_i^a\)

  • \(y(\lambda x_i) = (\lambda x_i)^a = \lambda^a x_i^a = \lambda^a y(x_i)\)

  • ➔ Power law

Laws of urban scaling

• Regularities

• Quantitative revolution post WW2

• Cultural turn

• … today …

Metcalfe’s law / Moore’s law

• As cities grow…

• … the number of potential connections increases as the square of population.

• \(C = p(p-1)/2 \propto p^2\)

von Thunen’s law

• As cities grow in size …

• land values decline non-linearly from the centre

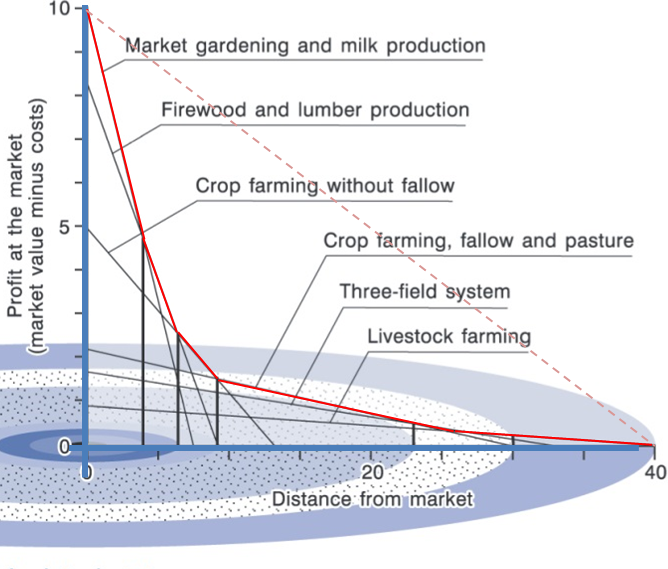
Source: Coe, Kelly, and Yeung (2019)

Law of gravitation / Tobler’s law

• As cities grow…

• .. interactions between them decline with increasing distance

• Newton law of gravitation

Source: I, Dennis Nilsson, CC BY 3.0, https://commons.wikimedia.org/w/index.php?curid=3455682

Zipf law

• As cities get larger…

• … there are less of them

• Regularity in the distribution of cities within a country

• Empirical observation and quantification

• Hierarchical urban systems:

  • one/a few big cities

  • more medium size cities

  • large number of very small cities

Zipf law

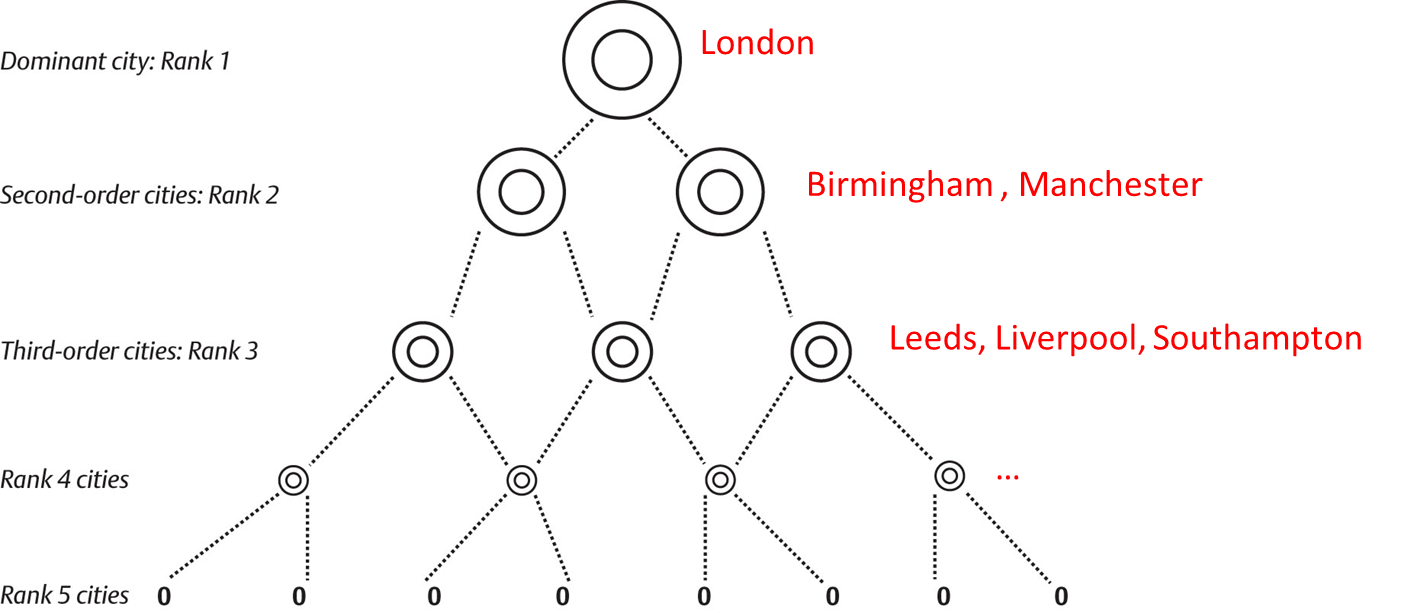
Zipf law

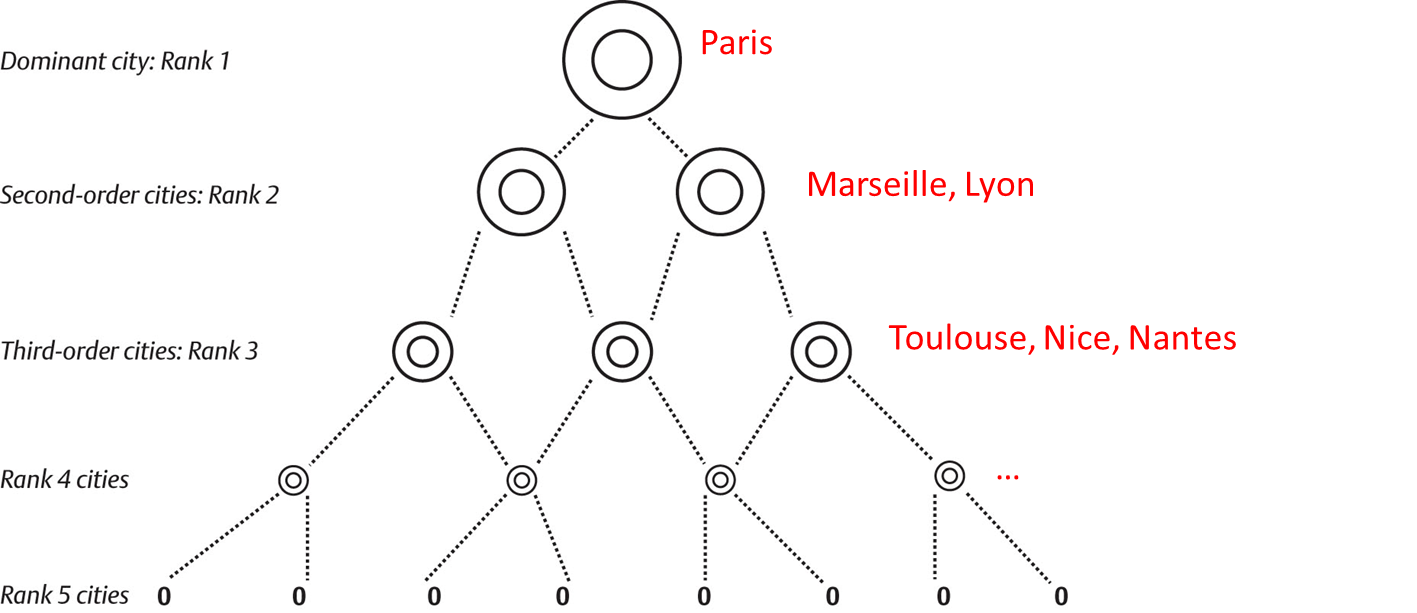
Zipf law

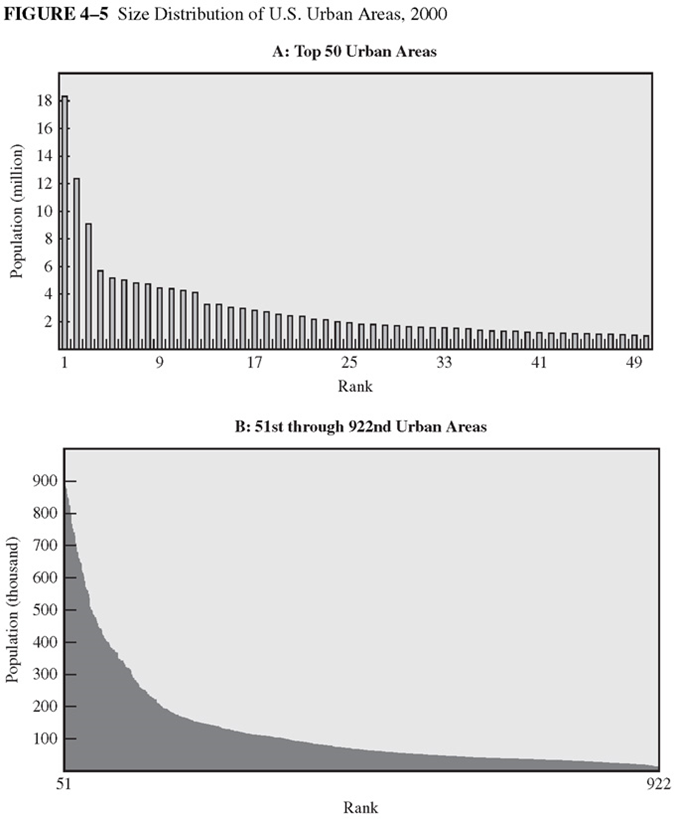
Source: O’sullivan (2012)

Rank size rule

\(pop_i = pop_d r_i^{-a}\)

if \(a=1\): Zipf law

\(pop_i = pop_d / r_i\)

Zipf law

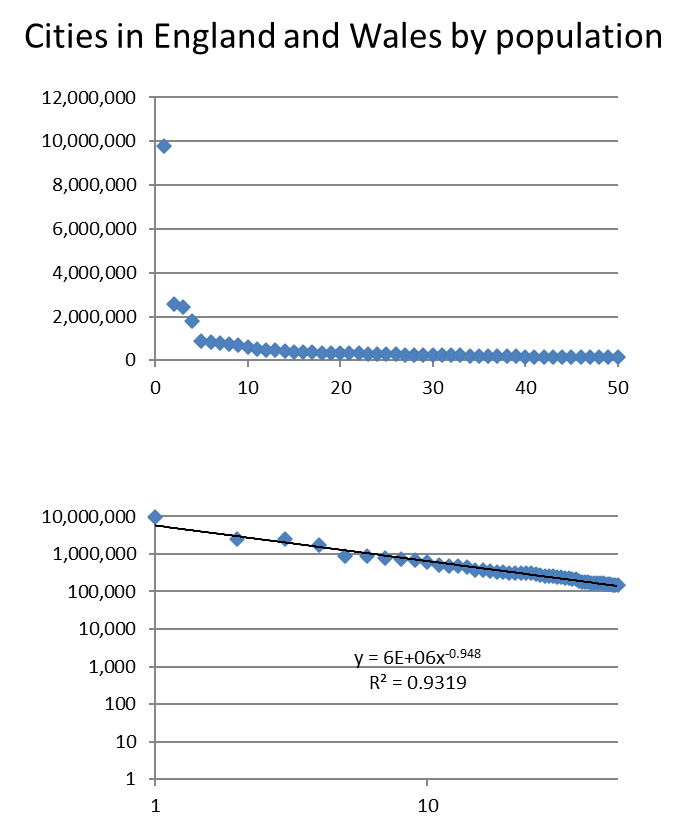
Rank size rule

\(pop_i = pop_d r_i^{-a}\)

if \(a=1\): Zipf law

\(pop_i = pop_d / r_i\)

Zipf law

• Primary cities above what a Zipf law would predict

• Newly industrialised countries

• No overall consensus why the rank-size rule holds

• Statistical regularity or an underpinning micro-economic process?

Bettencourt-West or Marshall’s law

• As cities grow…

• … their average real income (and wealth) increases more than proportionately (Bettencourt et al. 2007)

\(Y_i = Y_0P_i^\beta\)

• \(Y_i\): material resources (energy or infrastructure) or social activity (wealth, patents, and pollution) in city \(i\)

• \(Y_o\): normalization constant

• \(P_i\): population of city i

• \(\beta\): exponent

Bettencourt-West or Marshall’s law

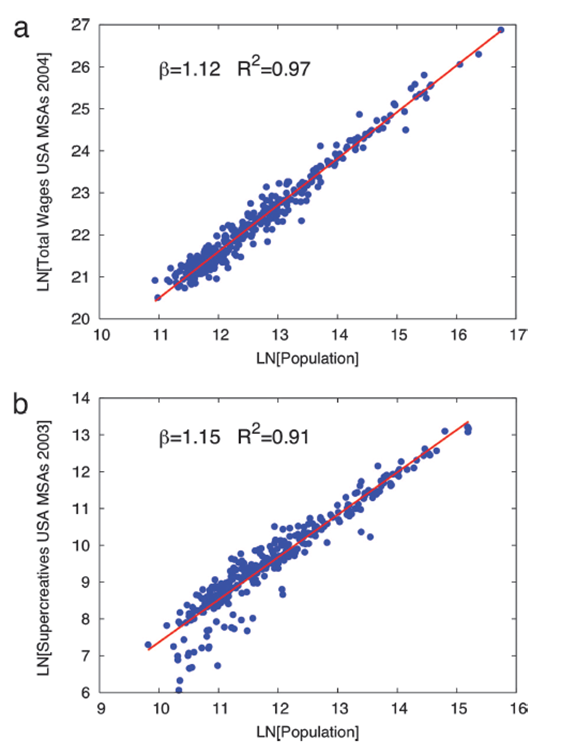
Source: Bettencourt et al. (2007)

• Not surprisingly another straight line

• Another power law

Bettencourt-West or Marshall’s law

Source: Bettencourt et al. (2007)

Bettencourt-West or Marshall’s law

An average urban dweller in the capital, Lisbon, has approximately twice as many reciprocated mobile phone contacts, k, as an average individual in the rural town of Lixa.

Source: Bettencourt (2021)

Bettencourt-West or Marshall’s law

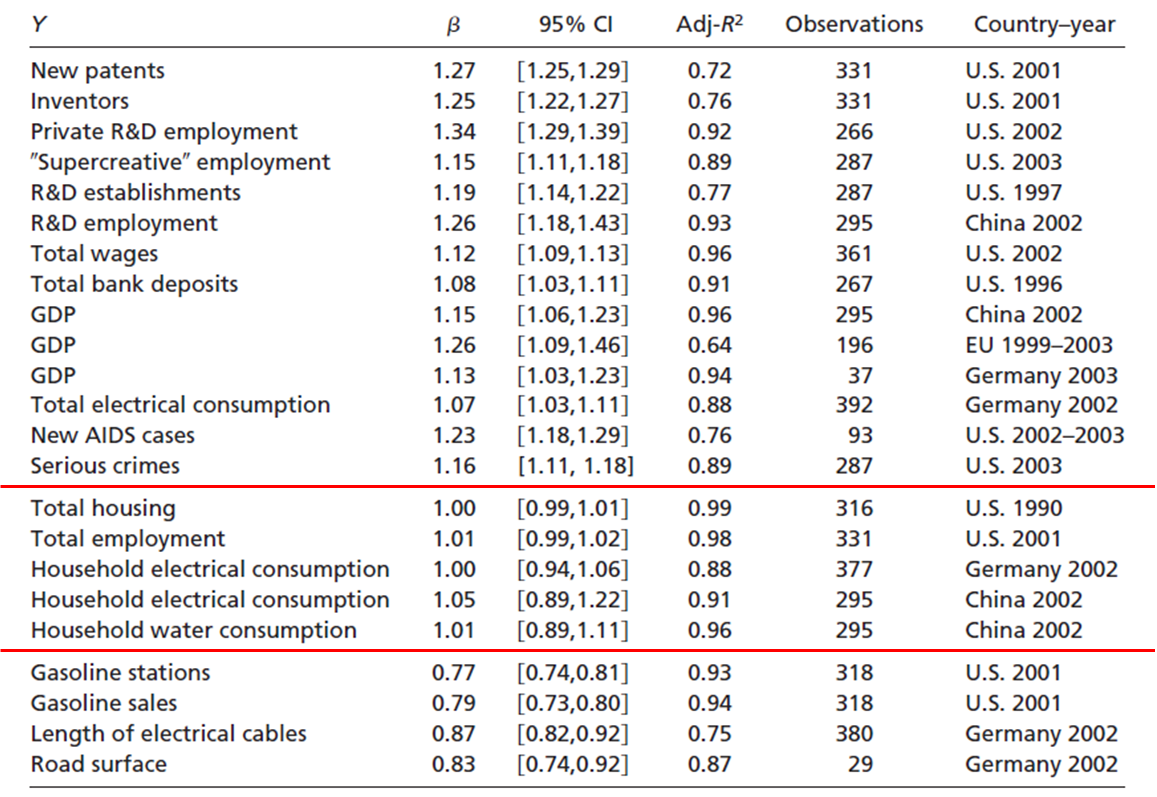
• \(Y=3P^b\)

• 300 random observation

• Plotting the results

• Economies of scale

• \(b<1\) decreasing returns to scale

• \(b=1\) constant returns

• \(b>1\) increasing returns

• SF networks, economies of scale?

Revisit economies of scale

Epilogue

Bettencourt (2021):

Cities, of course, do not really have their own dynamics; they depend on decisions made by people, corporations, governments, and others. The aggregate statistics of all their decisions will therefore emerge as key and provide another con- nection to the uses of information in urban science.

References

Albert, Réka, Hawoong Jeong, and Albert-László Barabási. 2000. “Error and Attack Tolerance of Complex Networks.” Nature 406 (6794): 378–82.

Barabási, Albert-László, and Réka Albert. 1999. “Emergence of Scaling in Random Networks.” Science 286 (5439): 509–12.

Batty, Michael. 2013. The New Science of Cities. MIT press.

Bettencourt, Luı́s MA. 2021. “Introduction to Urban Science: Evidence and Theory of Cities as Complex Systems.”

Bettencourt, Luı́s MA, José Lobo, Dirk Helbing, Christian Kühnert, and Geoffrey B West. 2007. “Growth, Innovation, Scaling, and the Pace of Life in Cities.” Proceedings of the National Academy of Sciences 104 (17): 7301–6.

Coe, Neil M, Philip F Kelly, and Henry WC Yeung. 2019. Economic Geography: A Contemporary Introduction. John Wiley & Sons.

Erdős, Paul, Alfréd Rényi, et al. 1960. “On the Evolution of Random Graphs.” Publ. Math. Inst. Hung. Acad. Sci 5 (1): 17–60.

O’sullivan, Arthur. 2012. “Urban Economics 8th Ed.”

Torres, Sonia H, Marı́a Montes de Oca, Eduardo Loeb, Priva Zabner-Oziel, Valentina Wallis, and Noelina Hernández. 2009. “Isoenzimas de Lactatodeshidrogenasa En El músculo Esquelético de Pacientes Con EPOC.” Archivos de Bronconeumologı́a 45 (2): 75–80.

Watts, Duncan J, and Steven H Strogatz. 1998. “Collective Dynamics of ‘Small-World’networks.” Nature 393 (6684): 440–42.